The beauty and complexity of chaos
Michael Gibb
?
Chaos does not have to be something scary or disturbing. According to Professor Ron Chen Guanrong, Chair Professor in the Department of Electronic Engineering at City University of Hong Kong (CityU), chaos offers the world visions of great complexity and beauty.
Professor Chen, one of CityU’s most distinguished scholars, took the 200-strong audience on a fascinating journey through the world of chaos theory in the latest installment of the President’s Lecture Series: Excellence in Academia on 12 March. Professor Chen is the director of CityU’s Centre for Chaos and Complex Networks and an IEEE Fellow. He has an h-index of 77.
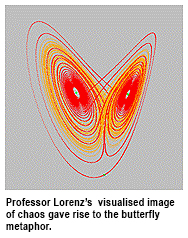
During his talk, he referenced the well-known “butterfly effect”, i.e. the metaphor of a butter?y famously ?apping its wings in Rio de Janeiro and ultimately causing a hurricane in Texas, as well as more esoteric research into the variation between chaos systems devised by renowned researchers in the field such as the famed US mathematician and meteorologist Professor Edward Lorenz and that of his own group, too.
The talk began with a description of the butter?y metaphor, as devised by Professor Lorenz in the early 1960s.
“[Professor Lorenz] discovered a meteorological model that today could explain this ‘butter?y effect’ and which formed the basis for the mathematical theory of chaos,” said Professor Chen. “We will show how we extended the chaotic Lorenz system to a family of in?nitely many genetically-related chaotic systems over the past decade.” Hence we have the title of the talk, “From One to Infinity”.
Professor Lorenz’s work provided the fundamental basis of the talk. As Professor Chen explained, Lorenz received the Kyoto Prize in 1991 for discovering “deterministic chaos,” a principle which has profoundly influenced a range of basic sciences and brought about a dramatic change in our view of nature.
For non-mathematicians present at the talk, Professor Chen defined chaos from the point of view of science, explaining how it can be regarded as dynamic movement that was “non-divergent, non-convergent and non-periodic”. Building on Lorenz’s original analysis, he showed that his own system, outlined in a 1999 paper titled “Yet another chaotic attractor” in the International Journal of Bifurcation and Chaos, was “as simple as the Lorenz system but has much more complicated dynamics”. This paper has received more than 1,350 citations since publication.
His presentation at CityU also included a thorough analysis of his own work, the Chen system, presenting the firm applications of his theories in terms of patents, circuits and a device called a Chaotic Mixer, which can mix liquids in such a way that the action of the mixer is non-divergent, non-convergent and non-periodic.
Professor Chen’s work in the field of chaos and complex networks earned him
the State Natural Science Award in 2008 and 2012 respectively, one of the highest honours in the field of science, technology and engineering in mainland China.
the State Natural Science Award in 2008 and 2012 respectively, one of the highest honours in the field of science, technology and engineering in mainland China.
Professor Chen peppered his talk with research tips and anecdotes about his career, aimed at motivating students and junior faculty. He urged colleagues to motivate themselves to work on important research problems, not to give up, think outside the box, collaborate with the best people in the field, to thoroughly analyse a particular problem, and approach publication shrewdly.
“Conceive attractive titles for your papers,” he said. “Write short papers for quick publication, and submit papers to journals with a large readership.” Longer papers could go into greater detail, he said.
He concluded by saying, “If you feel a research topic is important, try to work through it until you believe there is nothing left out for you to do. If you have already started to work on a significant topic, try to work out all important issues until you believe other people cannot do any more.”
Several members of the audience picked up on philosophical ideas that Professor Chen touched upon in his talk related to the number 1 and to the notion of the infinite, namely references to ancient Chinese wisdom presented in the I Ching and the concept of the Tao. Other questions concerned conceptual issues related to the mathematics underlying Professor Chen’s work and applications of chaos theory to everyday life.
?